拓扑排序(Topological sort)是针对有向无环图(Directed Acyclic Graph, DAG)的一种线性排序。在有向图中,如果存在一条 $u$ 指向 $v$ 的边,那么在拓扑排序中,$u$ 就排在 $v$ 的前面。
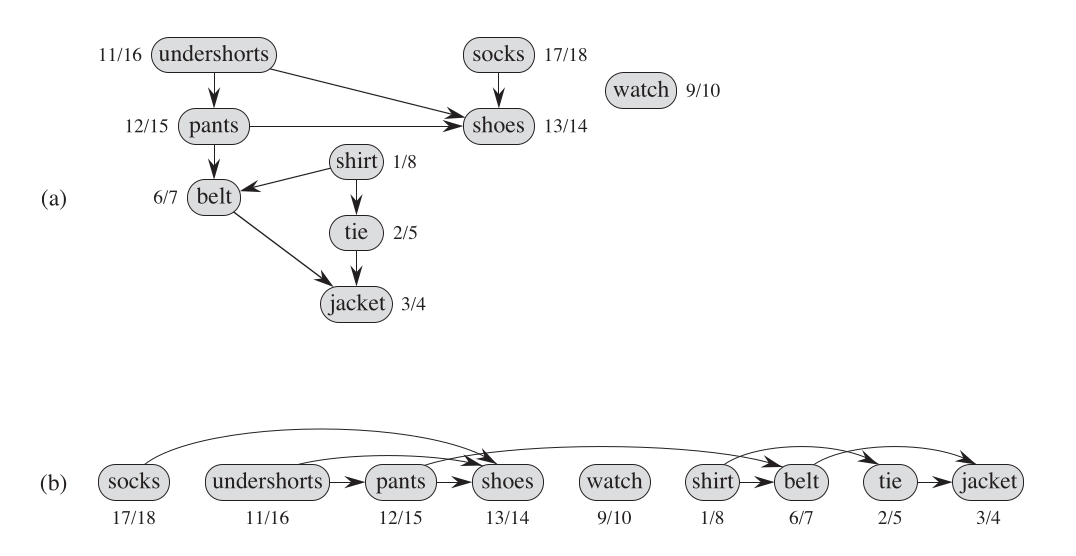
拓扑排序并不是通常意义的排序(如快排,桶排等),而是给一系列有先后顺序的事件排序,有点像游戏里的前置任务,选课时的先修课。CLRS 使用穿衣服的先后顺序,说明拓扑排序的应用场景。
#实现方法
- 调用 DFS(G) 遍历图,计算每个顶点 $u$ 的搜索结束时间 $u.f$。
- 每搜索完一个顶点,将这个顶点加入到链表的头部。
- 返回链表。
下面是 CLRS 中给出的伪代码,样例依然可以参考上图中穿衣服的例子。
拓扑排序的结果并不是唯一的。

#时间复杂度
$\Theta(V + E)$
因为在邻接表上 DFS 的时间复杂度是 $\Theta(V + E)$,在链表头部插入的时间开销是 $\mathcal{O}(1)$,所以总的时间复杂度是$\Theta(V + E)$。