#连通性
在无向图 $G$ 中,如果从顶点 $u$ 到顶点 $v$ 存在通路,则称 $u$ 和 $v$ 是连通的。
在有向图 $G$ 中,如果从 $u$ 到 $v$ 存在通路,从 $v$ 到 $u$ 也存在通路,则称 $u$ 和 $v$ 强连通。
#连通图
在无向图 $G$ 中,如果 $V(G)$ 中的任意两个顶点 $u$,$v$ 都是连通的,则称 $G$ 为连通图。
在有向图 $G$ 中,如果 $V(G)$ 中的每两个顶点都强连通,称 $G$ 是一个强连通图。
将有向图 $G$ 中所有的有向边替换为无向边,所得到的图 $G^{'}$ 称为原图 $G$ 的基图。如果一个有向图 $G$ 的基图 $G^{'}$ 是连通图,则有向图 $G$ 是弱连通图。
#子图
如果一个图 $G^{'}$ 的边集 $E^{'}(G^{'})$ 和点集 $V^{'}(G^{'})$ 分别是另一个图 $G$ 的边集 $E(G)$ 和点集 $V(G)$ 的子集,则称图 $G^{'}$ 是图 $G$ 的子图。如果图 $G^{'}$ 的边集或点集是真子集,则称图 $G^{'}$ 为真子图。
如果一个子图 $G^{'}$ 的顶点集与原顶点集相同,而边集是原图边集的子集,则称图 $G^{'}$ 是原图 $G$ 的生成子图(Spanning Subgraph)。
图 $G$ 顶点集 $V$ 的一个子集 $V^{'}$ 和该图中两顶点均在该子集的所有边的集合 $E^{'}$ 组成的图 $G^{'}$ 称为导出子图(Induced Subgraph)。
下面三个定义来自百度知道。
子图:从原图中删去一些点或删去一些线或既删去一些点又删去一些线,剩下的部分(当然必须仍然是图)。允许两种极端情况:什么都不删;删去所有点和所有线。
真子图:同“子图”,但不允许什么都不删。
生成子图:同“子图”,但只允许删去线,不允许删去点。
#连通分量
连通分量是无向图的概念。无向图的极大连通子图称为的连通分量(Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。
#连通分量的计算
无向图的连通分量计算简单,DFS 遍历图,在 DFS 森林中,每棵树就是一个连通分量。因此可以通过这种方法判断一个无向图是不是连通图:如果 DFS 遍历这个图只得到一棵树,就说明这个无向图是个连通图。
#强连通分量
强连通分量(Strongly Connected Components, SCC)是针对有向图来说的。一个有向图中所有的强连通顶点组成的子图,又叫极大强连通子图,就是强连通分量。一个有向图可以有很多强连通分量,一个强连通分量中的顶点间可以没有直接相连的边,但必须相互可达。下图的每个阴影区域,就是一个强连通分量。
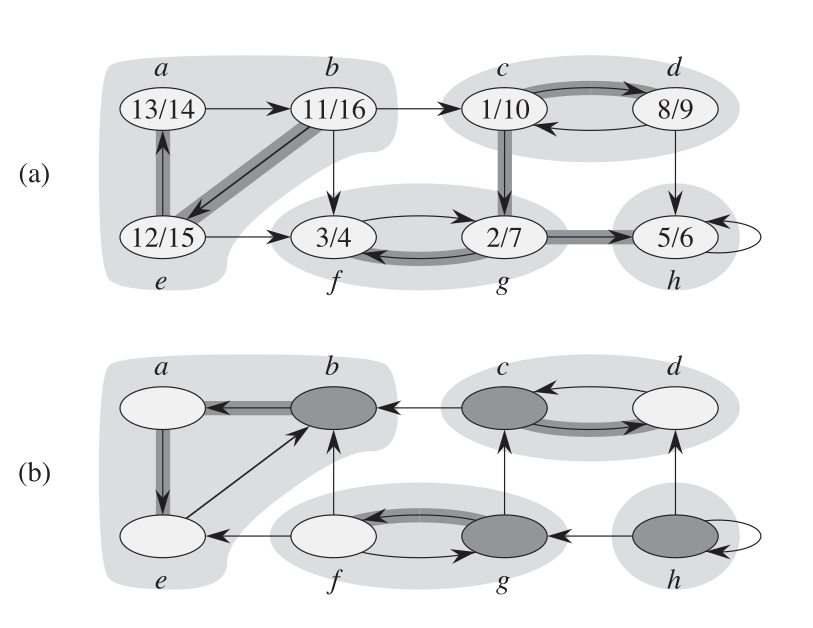
#强连通分量的计算
计算强连通分量,我们还需要得到有向图 $G$ 的转置图 $G^T$(或叫反图)。有向图的转置就是将所有的边反向,比如原图 $G$ 有从 $u$ 到 $v$ 的边,则转置图 $G^T$ 中有从 $v$ 到 $u$ 的边,$G^T = \{ V, E^T \}$。对于使用邻接表表示的有向图,计算其转置的时间复杂度为 $\mathcal{O}(V + E)$。上图的 $(a)$ 与 $(b)$ 互为转置。图 $G$ 和它的转置图 $G^{T}$ 具有相同的强连通分量,图 $G$ 的顶点 $u$ 和 $v$ 相互可达,当且仅当转置图 $G^{T}$ 中的顶点 $u$ 和 $v$ 相互可达。
下面介绍 Kosaraju 算法计算强连通分量,当使用邻接表表示图时,其时间复杂度为 $\Theta(V + E)$。
- 首先 DFS 遍历原图 $G$,记录每个顶点 $u$ 的结束时间 $u.f$
- 计算转置图 $G^T$
- 以第 1 步得到的顶点链表的顺序,即 $u.f$ 减小的顺序 DFS 遍历转置图 $G^T$
- 第 3 步 DFS 遍历得到的深度搜索森林,就是强连通分量,深度搜索树的数量就是强连通分量的数量
伪代码如下

看伪代码或者算法思想很难理解,建议手动计算一遍,加深印象,下图中的 $c$ 就是图 $a$ 的全部强连通分量。将强连通分量中的顶点看作一个顶点,生成的图叫 meta graph。
我们知道一个有向无环图(DAG)中,至少存在一个入度为 0 的顶点,称为 source node,至少存在一个出度为 0 的顶点,称为 sink node。在强连通分量中也有类似的概念,没有边进来的分量叫做 source component,没有边出去的分量叫 sink component。
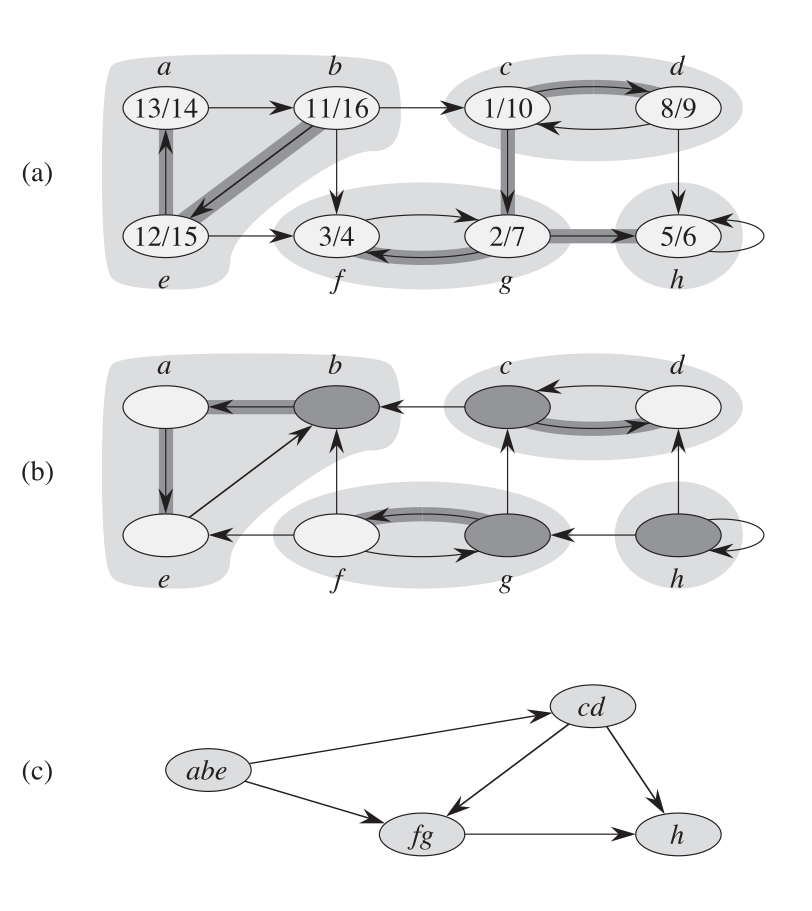
通过手动计算,可以更好地理解,所谓强连通分量,就是一个全部可达的子图,只要到达这个子图中的任意一个顶点,就可以到达这个子图中的所有顶点。强连通分量将原图分割为不同的区域,方便后续计算。