#图的两种主要表示方法
图有两种常用的表示方法,一种是邻接表法(adjacency-list),另一种是邻接矩阵法(adjacency-matrix)。
邻接表法储存数据更紧凑,适合稀疏的图(sparse graphs)
邻接矩阵法适合密集的图(dense graphs)
下图来自 CLRS,很好的展示两种不同的表示方法。
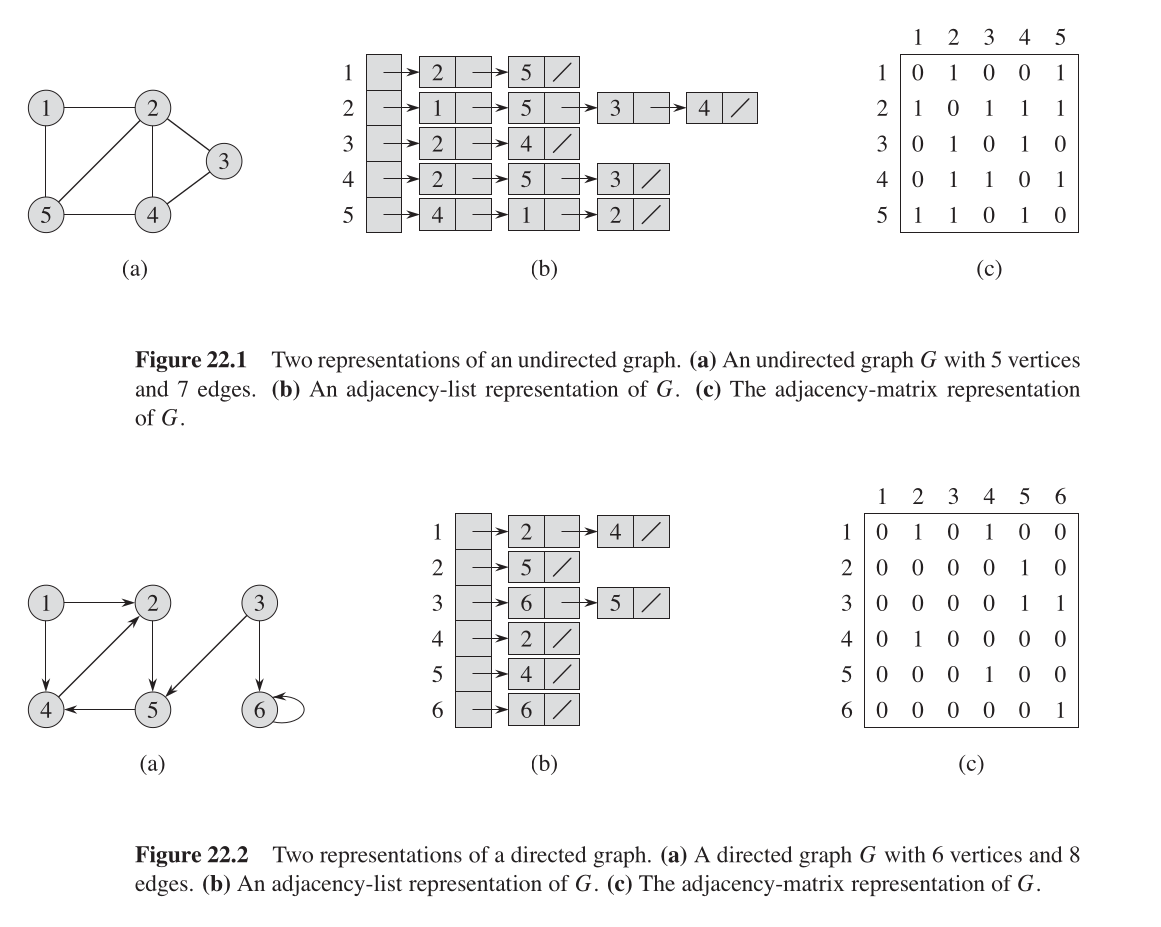
在邻接法表示中,一个图 $G = (V, E)$ 由含有 $|V|$ 个链表头的数组 $Adj$ 构成。每个链表包括相对应的顶点能直接到达的所有顶点。无向图的邻接表所有链表的长度和为 $2 |E|$,即边的个数的 2 倍,有向图的邻接表的所有链表长度和为 $|E|$。无论有向图还是无向图,邻接表法的空间复杂度都为 $\Theta(V + E)$。
邻接表的缺点是,它无法快速给出两个顶点间是否有直接相连的边。
邻接矩阵法使用一个 $|V| \times |V|$ 的矩阵表示图,如果两个顶点间有边,那么相对应的 $G[u][v]$ 值为 1(或者权重) ,否则为 0 。观察无向图的邻接矩阵,矩阵以主对角线为轴对称,因此我们几乎可以将无向图的邻接矩阵空间占用减半。无论有向图还是无向图,邻接矩阵法的空间复杂度都是 $\Theta(V^2)$ ,与边的个数无关
邻接表与邻接矩阵两种方法,可以清晰的体现,时间换空间,空间换时间,这种“计算守恒定律”(这句话是我自己编的)
#广度优先搜索 (又称宽度优先搜索,Breadth-First Fearch, BFS)
给定图 G = (V, E), 以及一个顶点 s,BFS会搜索所有可达的顶点,计算从初始 s 到目标顶点 t 的距离(距离指经过的边的数量)。BFS 还会生成一个广度优先树,以 s 为根,包括所有的可达顶点。对于图中的两个顶点 s 以及 t ,最短的路径就是以 s 为根的广度优先树中,根 s 到 t 的路径。
BFS 之所以叫 BFS,就是因为它“均匀” 的发现所有顶点,在距离初始顶点 s k + 1 距离的顶点被发现前,所有距离为 k 的顶点都已经被发现。BFS 在发现顶点时,使用颜色来标记,初始时所有的顶点都为白色,当一个顶点被发现时,它被标记为灰色(或者黑色),如果一个顶点是黑色,那么它周围直接连接的所有顶点,只能灰色或者黑色,而灰色顶点周围可以有白色顶点。
BFS 构建一个广度优先树,初始顶点为根。扫描已发现顶点 u 的邻接表,每当发现(第一次遇见)一个白色顶点 v 的时候,将顶点 v 以及边 (u, v) 加入到树,称顶点 u 为顶点 v 的在树中的前序顶点(predecessor)或者父顶点(parent)。因为一个顶点只能被发现一次,一个顶点最多有一个父顶点。在广度搜索树中,祖先顶点与孙子顶点是相对初始顶点 s 来说的。
BFS使用队列(Queue)实现,以下的代码来自 CLRS,图用邻接表来表示时,BFS 的时间复杂度是 $\mathcal{O}(V + E)$。

下面是 BFS 的例子,同样来自 CLRS。
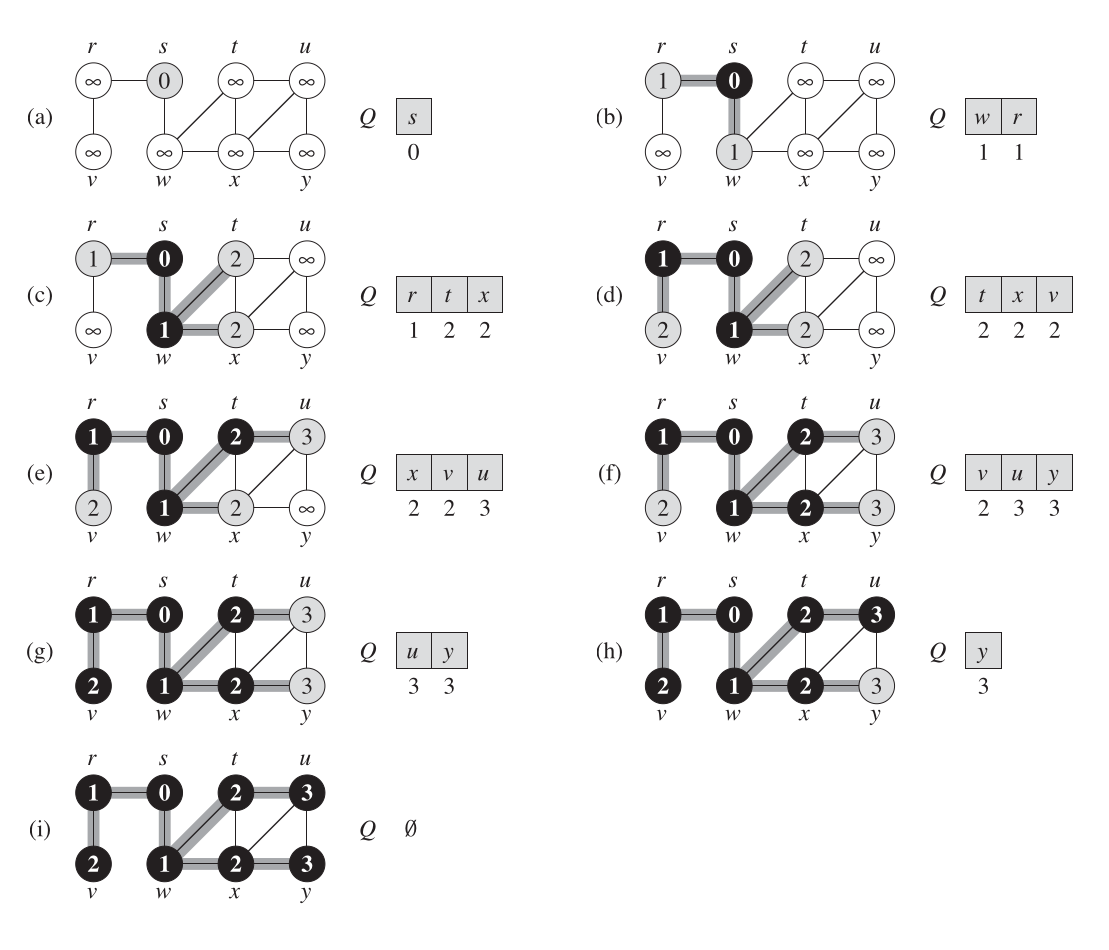
BFS 可以查找两顶点间的最短距离。
#深度优先搜索 (Depth-First Search, DFS)
深度优先搜索首先向更深处搜索,首先搜索最近发现的,还有未发现的边的顶点。一旦某个顶点的所有边都搜索完毕,就回溯,直到所有的可达的顶点都被搜索到。如果依旧有未发现的顶点,DFS 选取一个未搜索顶点作为新的初始顶点,继续搜索,直到所有的顶点都被搜索。
对比广度优先与深度优先,你可能会发现(认为),BFS 只能搜索某个初始顶点的所有可达顶点而 DFS 搜素所有顶点。其实并不是这样,BFS 也可以选取其他初始顶点继续搜索,但是我们一般不这样做。BFS 通常用来寻找最短路径,而 DFS 通常作为遍历图的一种方法。两者应用场景不同。
因为 DFS 默认搜索所有的顶点,最后我们可能会得到一片深度搜索树森林。与广度优先一样,未发现的顶点为白色,正在探索的顶点为灰色,完全探索的顶点为黑色。深度优先搜索对每个被搜索的顶点 $v$,会记录两个时间,一个是搜索这个顶点的开始时间 $v.d$,另一个是搜索完毕当前顶点的时间 $v.f$,当 $t < v.d$ 时,顶点为白色,当 $v.d < t < v.f$ 时,顶点为灰色,当 $v.f < t$ 时,顶点为黑色。
下面是 CLRS 中 DFS 的伪代码。

CLRS 中 DFS 过程例子。
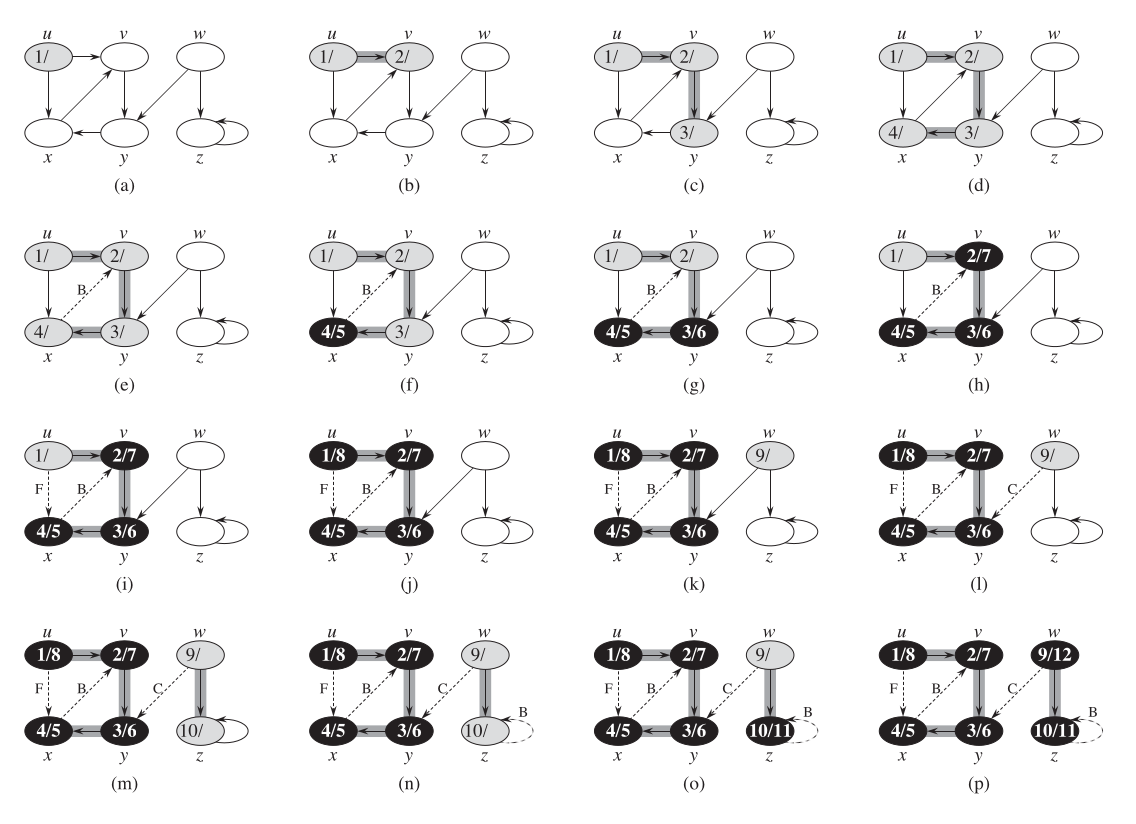
图用邻接表来表示时,DFS 的时间复杂度是 $\Theta(V + E)$。