$\mathcal{O}$ 记号是算法的上界,我们通常采用的是渐进的分析方法(Asymptotic analysis),即存在足够大的 $n$, 对于规模为 $n$ 的输入,算法需要的基本操作次数为 $\mathcal{O}(n)$。
对于某个函数 $T(n)$, 存在某个常数 $c$, 当 $n$ 足够大的时候,有 $T(n) < c * f(n)$, 那么这个函数 $T(n)$ 就是 $\mathcal{O}(f(n))$ 的。
需要注意的是,$\mathcal{O}(n)$ 并不总是大于 $T(n)$,因为 $O(n)$ 可以有常系数 $c$ 。例如,$T(3n + 1)$ 是 $\mathcal{O}(n)$ 的算法。
同时,还有 $\Theta$ 记号和 $\Omega$ 记号,$\Omega$ 是下界,是最好的情况,$\Theta$ 是确界。
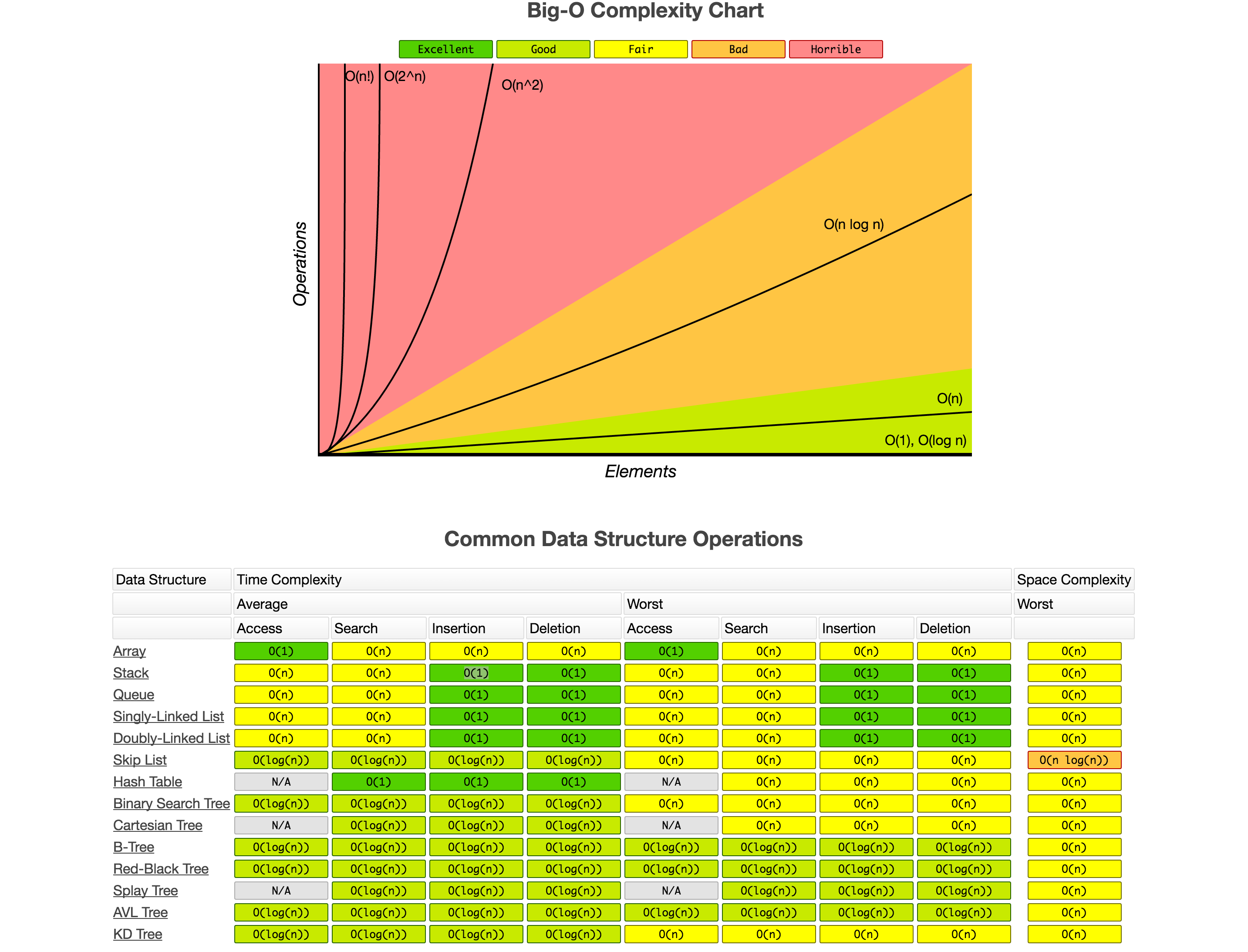
常见的复杂度类型:
$\mathcal{O}(1)$ , $\mathcal{O}(\log(n))$ , $\mathcal{O}(n^c)$ 。这样的时间复杂度的问题,我们认为是容易解的问题。
$\mathcal{O}(a^n)$, 例如 $\mathcal{O}(2^n)$ ,是难解的问题,这类算法的计算成本增长极快,通常认为是不可以忍受的。
一个 $\mathcal{O}(a^n)$ 的例子: $sum(a) = 2m, \exists b \subseteq a, sum(b) = m? $