Database Design Theory - Normalization

One of the great tools I found useful for learning normal form:
http://www.ict.griffith.edu.au/normalization_tools/normalization/ind.php

#Design

Relational database design requires that we find a "good" collection of relation schemas. A bad design may lead to

• Repetition of Information.
• Inability to represent certain information.

Design Goals:

• Avoid redundant data
• Ensure that relationships among attributes are properly represented
• Facilitate the checking of updates for violation of database integrity constraints

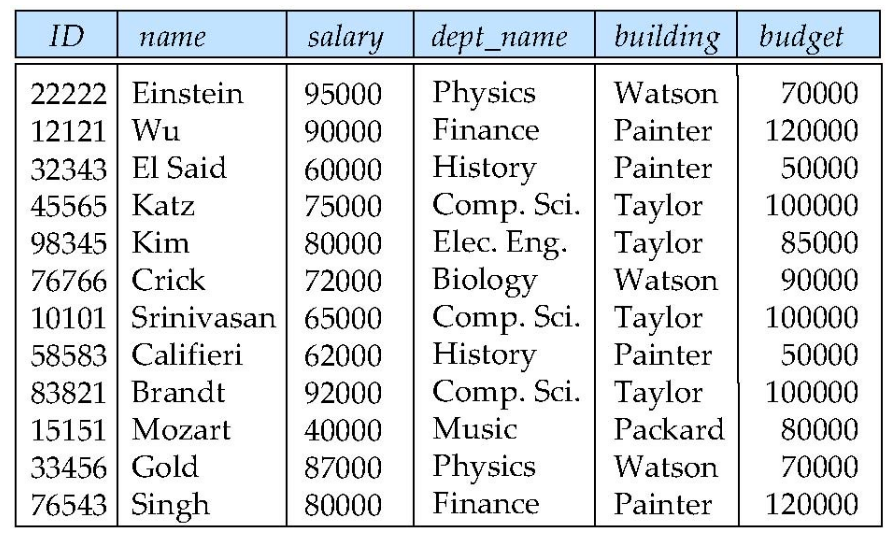An example of bad database design

Suppose we had started with inst_dept. How would we know to split up (decompose) it into instructor and department?

Write a rule "If there were a table (dept_name, building, budget), then dept_name would be a candidate key"

Denote as a functional dependency: dept_name $\rightarrow$ building, budget

In inst_dept, because dept_name is not a candidate key, the building and budget of a department may have to be repeated.

• This indicates the need to decompose inst_dept

Not all decompositions are good. Suppose we decompose

employee(ID, name, street, city, salary)

into

employee1 (ID, name)
employee2 (name, street, city, salary)

• This loses information -- we cannot reconstruct the original employee relation -- and so, this is a lossy decomposition.

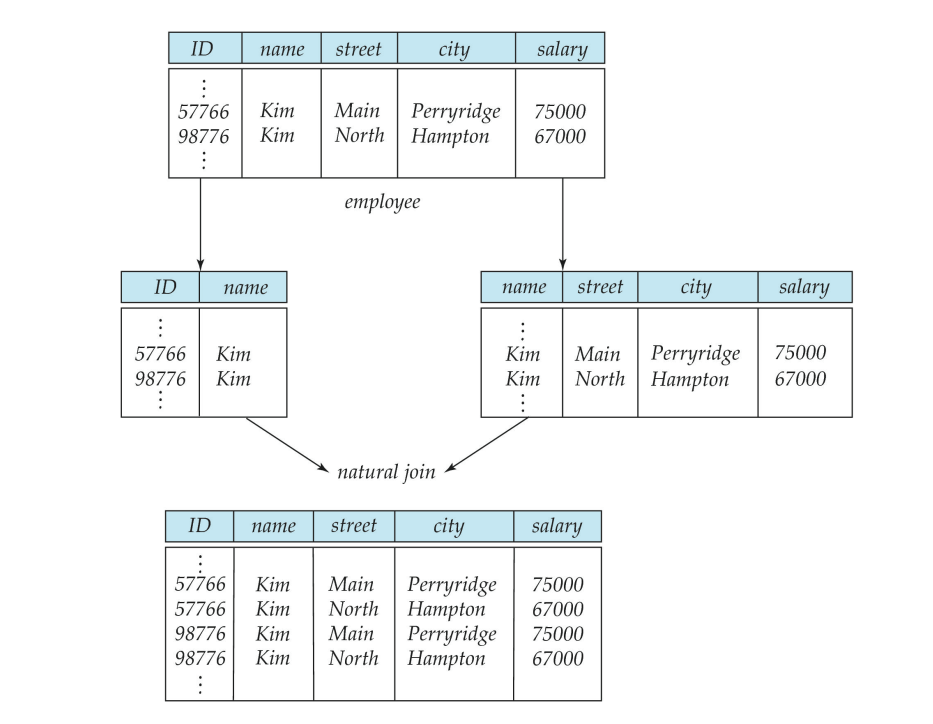An example of lossy decomposition

And please be careful, you cannot decide this by just looking at the data!

#First Normal Form

Domain is atomic if its elements are considered to be indivisible units

• Examples of non-atomic domains:
  • Set of names, composite attributes
  • Identification numbers like CS101 that can be broken up into parts

A relational schema R is in first normal form if the domains of all attributes of R are atomic

Non-atomic values complicate storage and encourage redundant (repeated) storage of data

• Example: Set of accounts stored with each customer, and set of owners stored with each account
• We assume all relations are in first normal form

#Goal — Devise a Theory for the Following

Decide whether a particular relation R is in "good" form.

If a relation R is not in "good" form, decompose it into a set of relations {R1, R2, ..., Rn} such that

• each relation is in good form
• the decomposition is a lossless-join decomposition

Our theory is based on:

• functional dependencies
• multivalued dependencies

#Functional Dependencies

Let R be a relation schema $$ \alpha \subseteq R \; and \; \beta \subseteq R $$ The functional dependency $$ \alpha \rightarrow \beta $$ holds on R if and only if for any relation r(R), whenever any two tuples $t_1$ and $t_2$ of $r$ agree on the attributes $\alpha$, they also agree on the attributes $\beta$. That is $$ t_1[\alpha] = t_2 [\alpha] \rightarrow t_1[\beta] = t_2 [\beta] $$

K is a superkey for relation schema R if and only if $K \rightarrow R$
K is a candidate key for R if and only if

• K $\rightarrow$ R, and
• for no $ \alpha \subset$ K, $\alpha \rightarrow$ R

Functional dependencies allow us to express constraints that cannot be expressed using superkeys. Consider the schema:
inst_dept (ID, name, salary, dept_name, building, budget )
We expect these functional dependencies to hold:
dept_name $\rightarrow$ building
and
ID $\rightarrow$ building
but would not expect the following to hold:
dept_name $\rightarrow $ salary

#Closure of a Set of Functional Dependencies

Given a set F of functional dependencies, there are certain other functional dependencies that are logically implied by F.
If A $\rightarrow$ B and B $\rightarrow$ C, then we can infer that A $\rightarrow$ C

The set of all functional dependencies logically implied by F is the closure of F.

• We denote the closure of F by $F^{+}$.
• $F^{+}$ is a superset of F.

#Boyce-Codd Normal Form

A relation schema R is in BCNF with respect to a set F of functional dependencies if for all functional dependencies in $F^{+}$ of the form where a $\subseteq$ R and b $\subseteq$ R, at least one of the following holds:

• $\alpha \rightarrow \beta$ is trivial (i.e., $\beta \subseteq \alpha$)
• $\alpha$ is a superkey for R

Example schema not in BCNF:
instr_dept (ID, name, salary, dept_name, building, budget )
because dept_name $\rightarrow$ building, budget
holds on instr_dept, but dept_name is not a superkey

#Decomposing a Relation into BCNF

Suppose we have a schema R and a non-trivial dependency $\alpha \rightarrow \beta$ causes a violation of BCNF. We decompose R into: $$ (\alpha \cup \beta) $$ $$ (R - (\beta - \alpha)) $$

• In our example,
• $\alpha$ = dept_name
• $\beta$ = building, budget and inst_dept is replaced by
• $(\alpha \cup \beta)$ = ( dept_name, building, budget )
• $(R - (\beta - \alpha))$ = ( ID, name, salary, dept_name )

#BCNF and Dependency Preservation

Constraints, including functional dependencies, are costly to check in practice unless they pertain to only one relation.

If it is sufficient to test only those dependencies on each individual relation of a decomposition in order to ensure that all functional dependencies hold, then that decomposition is dependency preserving.

Because it is not always possible to achieve both BCNF and dependency preservation, we consider a weaker normal form, known as third normal form.

#Third Normal Form

A relation schema R is in 3rd normal form (3NF) if for all $a \rightarrow b \text{ in }F^{+}$, at least one of the following holds

• $\alpha \rightarrow \beta$ is trival
• $\alpha$ is a superkey for R
• Each attribute A in $\beta - \alpha$ is contained in a candidate key for R

If a relation is in BCNF it is in 3NF.

Third condition is a minimal relaxation of BCNF to ensure dependency preservation

#Goals of Normalization

Let R be a relation scheme with a set F of functional dependencies.

Decide whether a relation scheme R is in "good" form.

In the case that a relation scheme R is not in "good" form, decompose it into a set of relation scheme {R1, R2, ..., Rn} such that

• each relation scheme is in good form
• the decomposition is a lossless-join decomposition
• Preferably, the decomposition should be dependency preserving.

#Functional-Dependency Theory

We now consider the formal theory that tells us which functional dependencies are implied logically by a given set of functional dependencies.

We then develop algorithms to generate lossless decompositions into BCNF and 3NF

We then develop algorithms to test if a decomposition is dependency-preserving

#Closure of a Set of Functional Dependencies

Given a set F set of functional dependencies, there are certain other functional dependencies that are logically implied by F.
e.g. If A $\rightarrow$ B and B $\rightarrow$ C, then we can infer that A $\rightarrow$ C
The set of all func. dependencies logically implied by F is the closure of F.
We denote the closure of F by $F^{+}$.

We can find $F^{+}$, the closure of F, by repeatedly applying Armstrong’s Axioms:

• if $\beta \subseteq \alpha$, then $a \rightarrow b$ (reflexivity)
• if $a \rightarrow b$, then $\gamma \alpha \rightarrow \gamma \beta$ (augmentation)
• if $a \rightarrow b$, and $\beta \rightarrow \gamma$, then $\alpha \rightarrow \gamma$ (transitivity)

Additional rules:

• If $\alpha \rightarrow \beta$ holds and $\alpha \rightarrow \gamma$ holds, then $\alpha \rightarrow \beta \gamma$ holds (union)
• If $\alpha \rightarrow \beta \gamma$ holds, then $\alpha \rightarrow \beta$ holds and $\alpha \rightarrow \gamma$ holds (decomposition)
• If $\alpha \rightarrow \beta$ holds and $\beta \gamma \rightarrow \delta$ holds, then $\alpha \gamma \rightarrow \delta$ holds (pseudotransitivity)

There are several uses of the attribute closure algorithm:

• Testing for superkey:
  • To test if a is a superkey, we compute a+, and check if a+ contains all attributes of R.
• Testing functional dependencies
  • To check if a functional dependency a ® b holds (or, in other words, is in F+), just check if b Í a+.
  • That is, we compute a+ by using attribute closure, and then check if it contains b.
  • Is a simple and cheap test, and very useful
• Computing closure of F
  • For each g Í R, we find the closure g+, and for each S Í g+, we output a functional dependency g ® S.

#Canonical Cover

Sets of functional dependencies may have redundant dependencies that can be inferred from the others

Intuitively, a canonical cover of F is a "minimal" set of functional dependencies equivalent to F, having no redundant dependencies or redundant parts of dependencies

A canonical cover for F is a set of dependencies $F_c$ such that -F logically implies all dependencies in $F_c$, and -$F_c$ logically implies all dependencies in F, and -No functional dependency in $F_c$ contains an extraneous attribute, and -Each left side of functional dependency in $F_c$ is unique.