Normal distribution, also known as Gaussian, Gauss, or Laplace-Gauss distribution, is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
$$ f(x) = \frac{1}{} $$ $$ \frac{\partial \rho}{\partial t} + \nabla \cdot \vec{j} = 0 $$
The graph depiction of normal distribution is called bell curve, because it looks like a bell.
#Empirical Rule
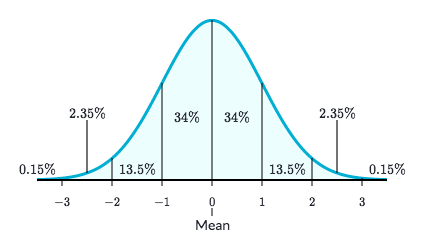
The empirical rule, alse referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, almost all observed data will fall within three standard deviations (denoted by $/sigma$) of the mead(denoted by $/mu$).
The empirical rule, also referred to as the three-sigma rule or 68-95-99.7 rule, is a statistical rule which states that for a normal distribution, almost all observed data will fall within three standard deviations (denoted by σ) of the mean or average (denoted by µ).
In particular, the empirical rule predicts that 68% of observations falls within the first standard deviation (µ ± σ), 95% within the first two standard deviations (µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).