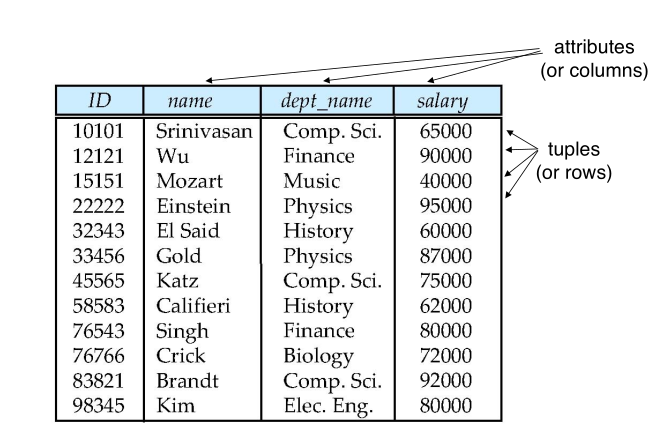
Example of a Relation
#Attribute Types
- The set of allowed values for each attribute is called the domain of the attribute
- Attribute values are (normally) required to be atomic; that is, indivisible
- The special value null is a member of every attribute
- The null value causes complication in the definition of many operations
#Relation Schema and Instance
- $A_1, A_2, \cdots, A_n$ are attributes
- $R = (A_1, A_2, \cdots, A_n)$ is a relation schema Example: instructor = (ID, name, dept_name, salary)
- Formally, given sets $D_1 ,D_2, \cdots, D_n$ a relation r is a subset of $D_1 \times D_2 \times \cdots \times D_n$ Thus, a relation is a set of n-tuples($a_1, a_2, \cdots, a_n$) where each $a_i \in D_i$
- The current values(relation instance) of a relation are specified bu a table
- An element t of r is a tuple, represented by a row in a table
#Relations are Unordered
- Order of tuples is irrelevant (tuples may be stored in an arbitrary order)
- This is on the logical design level - ordering can be defined on physical level
- A database consists of multiple relations
- Information about an enterprise is broken up into parts instructor, student, advisor
- Bad design: univ (instructor_id, name, dept_name, salary, student_id, ...)
results in
- repetition of information (e.g., two student have the same instructor)
- the need for full values (e.g., represent a student with no advisor)
- Normalization theory deals with how to design "good" relational schemas(What is good)
#Keys
superkey: K is a superkey of R if values for K are sufficient to identify a unique tuple of any possible relation r(R)
- Example: {id} and {id, name} are both superkeys of instructor.
- However, {name} is not a superkey.
candidate key: Superkey K is a candidate key if K is minimal
- Example: {id} is a candidate key for instructor
primary key One of the candidate keys is selected to be the primary key.
foreign key constraint: Value in one relation must appear in another
- Referencing relation
- Referenced relation
#Schema Diagram for University Database
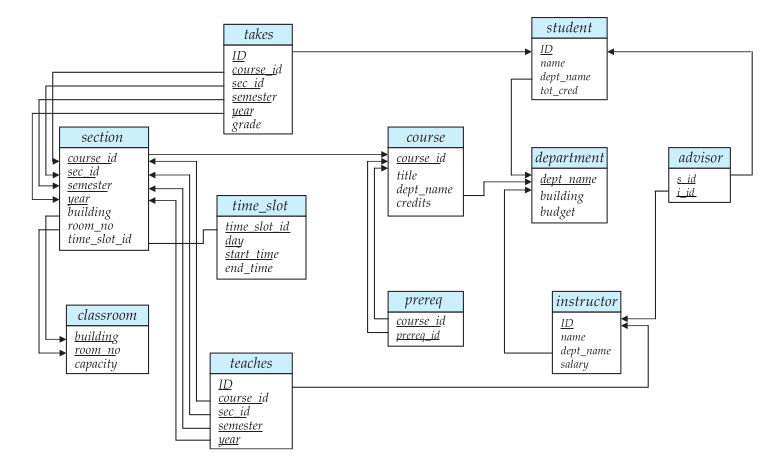Schema Diagram Example
This is a diagram of a relational design, it it not the same as the ER diagrams.