#Relational Algebra
- Procedural language
- Based on relational operations
- Three set of RA operations
- Basic RA operations
- select, project, union, set diff, cartesian product, rename
- Additional RA operations
- Can be expressed using basic ones
- But make it easier to write queries
- intersection, assignment joins, division
- Extended RA
- Increases power of RA
- Cannot be expressed with basic RA
- Aggregation and group_by
- Basic RA operations
#Relational Operators
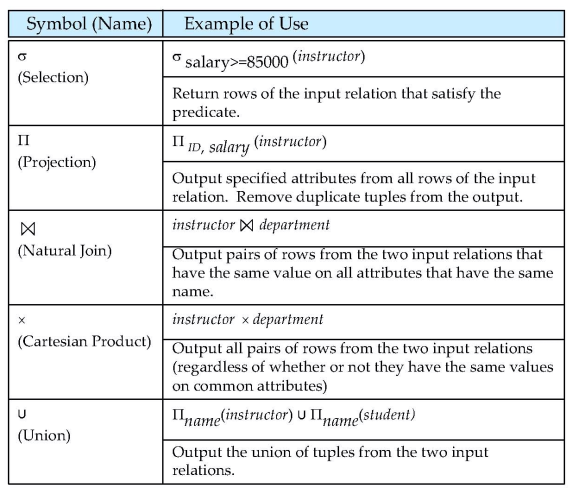
Six basic operators:
- select : $\sigma$
- project: $\Pi$
- union: $\cup$
- set difference: $-$
- Cartesian product: $\times$
- rename: $\rho$
All operators take one or two relations as input and produce a new relation as a result Addition operators defined on top of these six
#Basic RA operators
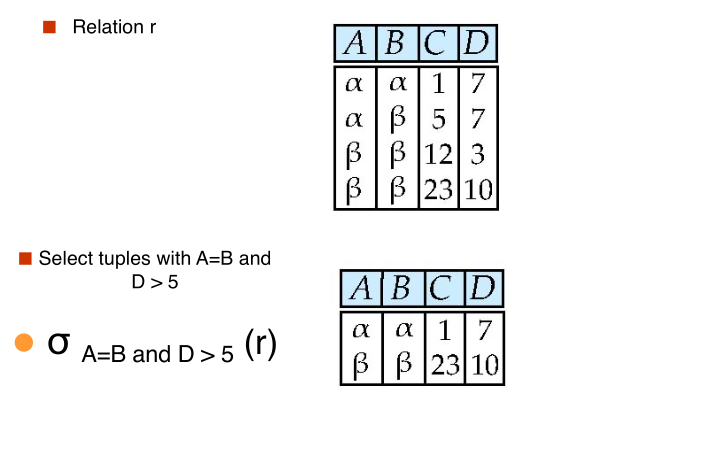
#select
$$ \huge \sigma_{\text{A = B and D > 5}}(r) $$

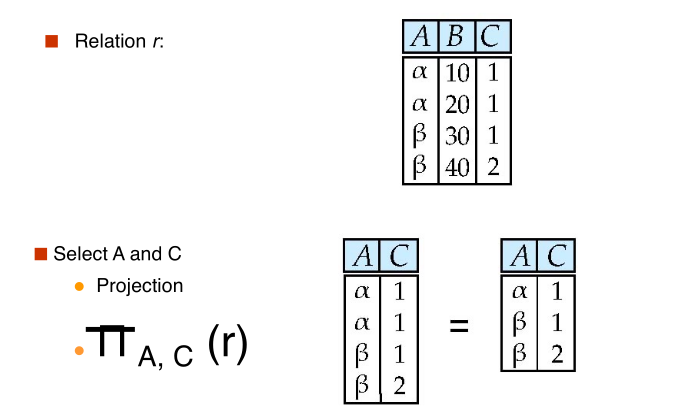
#project
$$ \huge \Pi_{A, C} (r) $$

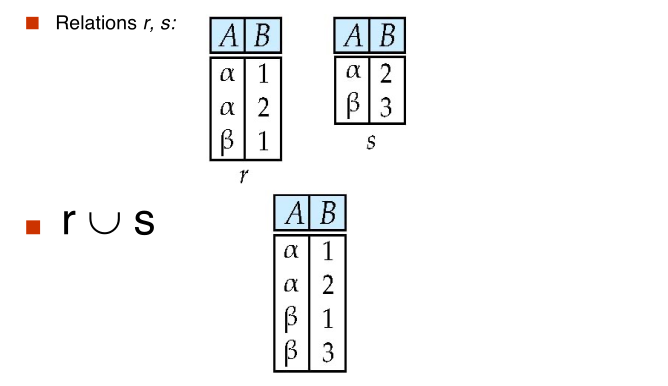
#union
$$ \huge r \cup s $$
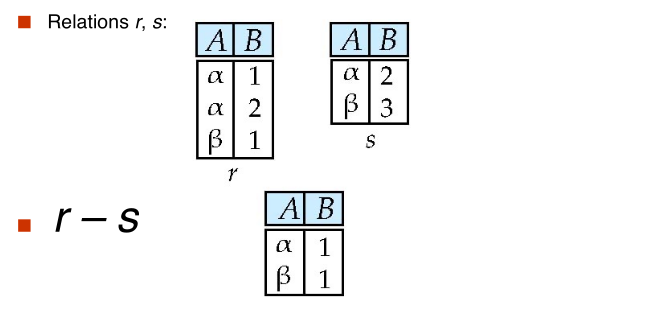
#set difference
$$ \huge r - s $$
#Cartesian Product
$$ \huge r \times s $$
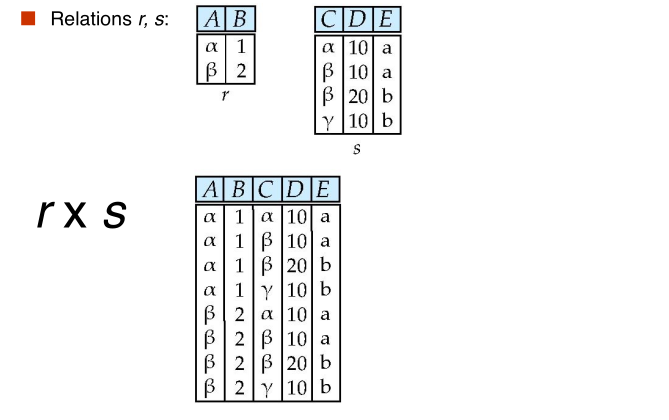

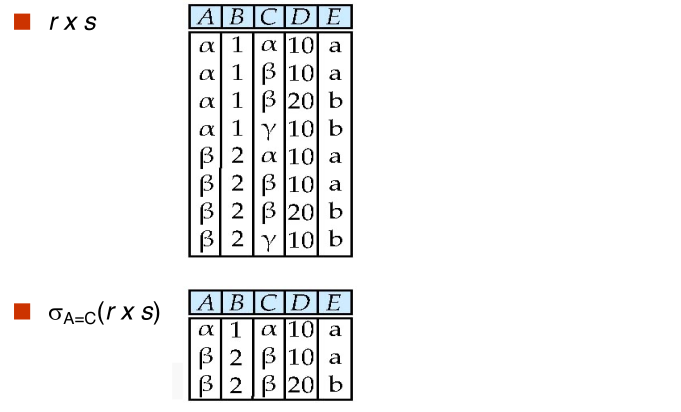
#composition of operations
Can build expressions using multiple operations Example: $\sigma_{A = C}(r \times s)$
#rename
Allow us to rename, and therefore to refer to, the results of relational algebra expressions.
Allow us to refer to a relation by more than one name.
example: $\rho_X(E)$ returns the expression E under the name X
If a relation-algebra expression E has arity n, then $$ \large \rho_{X(A_1, A_2, \cdots, A_n)}(E) $$ returns the result of expression E under the name X, and with the attributes renamed to $A_1, A_2, \cdots, A_n$
Example: Give relation CAKE(cname, price, slices) $$ \large \rho_{cheapcake(cakename, price, slices)}(\sigma_{price < 10}(CAKE)) $$
#Formal Definition
A basic expression in the relational algebra consists of either one of the following:
- A relation in the database
- A constant relation
Let $E_1$ and $E_2$ be relational-algebra expressions; the following are all relational-algebra expressions:
$$ E_1 \cup E_2 $$ $$ E_1 - E_2 $$ $$ E_1 \times E_2 $$ $$ \sigma_{p}(E_1) $$ $$ \Pi_{s}(E_1) $$ $$ \rho_{X}(E_1) $$
#Additional Operations
We define additional operations that do not add any power to the relational algebra, but that simplify common queries
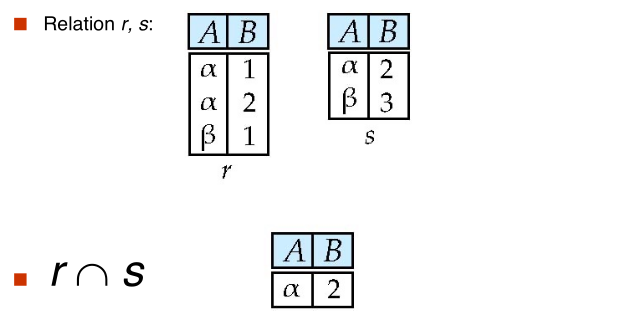
#set intersection
$$ \huge r \cap s $$
#natural Join
Let r and s be relations on schemas R and S respectively. Then, the "natural join" of relations R and S is a relation on schema $R \cup S$ obtained as follows:
- Consider each pair of tuples $t_r$ from r and $t_s$ from s
- If $t_r$ and $t_s$ have the same value on each of the attributes in $R \cap S$, add a tuple $t$ to the result, where
- $t$ has the same value as $t_r$ on r
- $t$ has the same value as $t_s$ on s
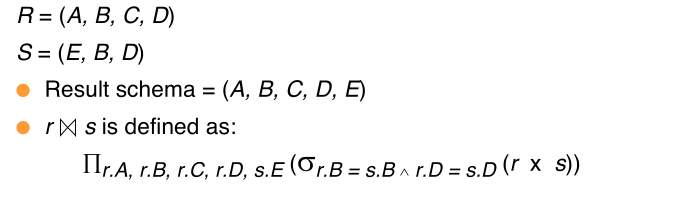
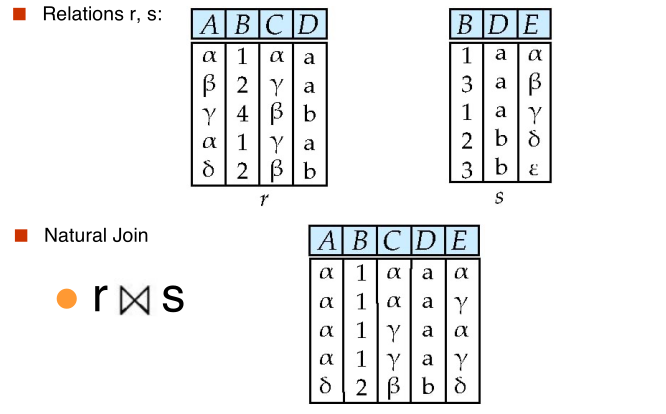
#natural join and theta join

#assignment
The assignment operation ($\leftarrow$) provides a convenient way to express conples queries.
Write query as sequential program consisting of
- a series of assignments
- followed by an operation whose value is displayed as a result of the query
Assignment must always be made to a temporary relation variable
Motivation from algebra
#outer join
An extension of the join operation that avoids loss of information
Computes the join and then adds tuples from one relation that does not match tuples in the other relation to the result of the join
Uses null values:
- null signifies that hte value is unknown or does not exist
- All comparisons involving null are(roughly speaking) false by definition
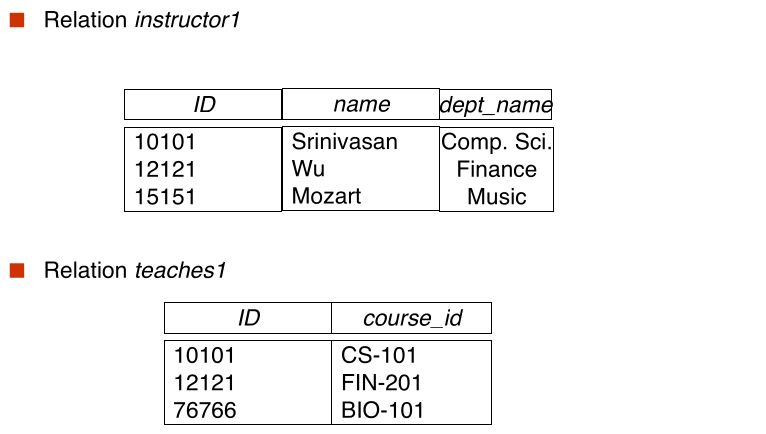
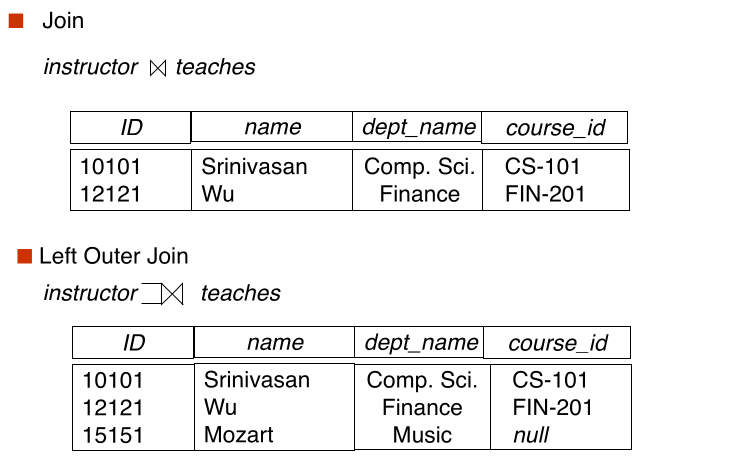
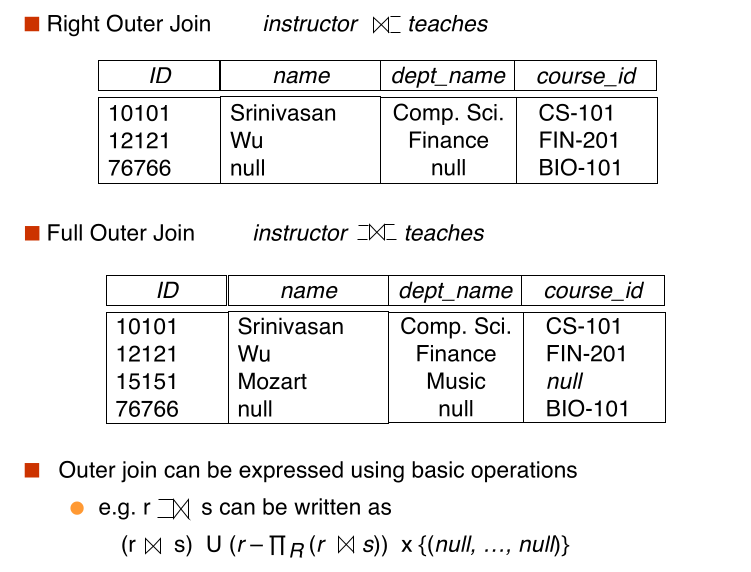
#Different join: theta vs natural vs outer join
Demo relation: Customer(cid, cname, joindate) purchase(cid, pid, buydate)
theta join: more general than natural join
natural join: special case, join on common attributes
works 95% of time, but what is we use "date" in both?
inner versus outer join is separate issue
#null values
- It is possible for tuples to have a null value, denoted by null, for some of their attributes
- null signifies an unknown value or that a value does not exist(yet)
- The result of any arithmetic expression involving null is null.
- Aggregate functions simply ignore null values
- For duplicate elimination and grouping, null is treated like any other values, and two nulls are assumed to be the same
- Comparisons with null values return the special truth value: unknown
- Three-valued login using the truth value unknown:
- or:
- (unknown or true) = true
- (unknown or false) = unknown
- (unknown or unknown) = unknown
- and;
- (unknown and true) = unknown
- (unknown and false) = false
- (unknown and unknown) - unknown
- not:
- (not unknown) = unknown
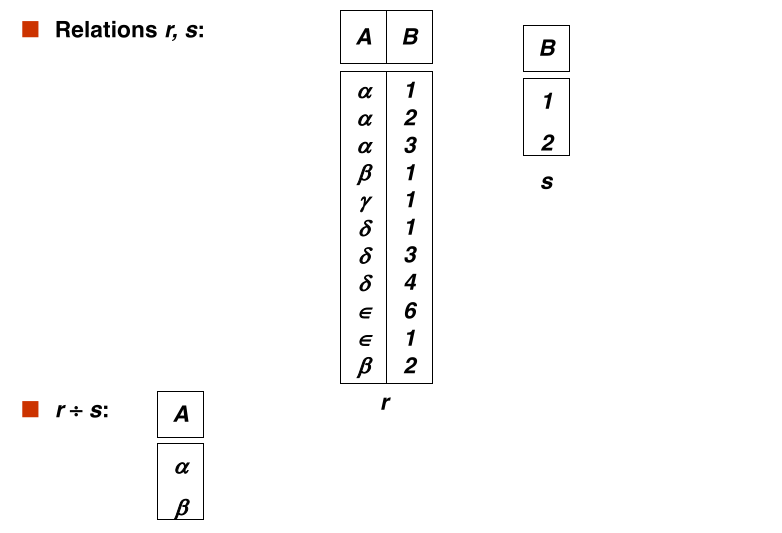
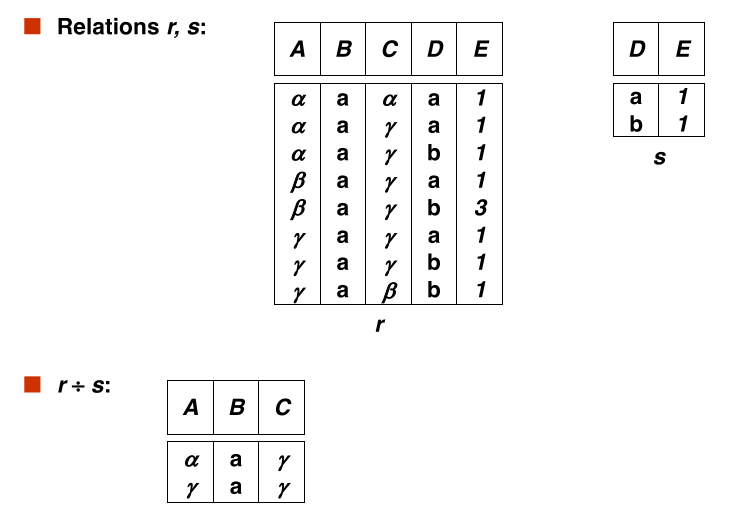
#division
Given relation r(R) and s(S), such that $S \subset R$, $r \div s$ is the largest relation t(R - S) such that $t \times S \subseteq r$
Example:
let $$ \large r(ID, course_id) = \Pi_{ID, course_id}(takes) $$ and $$ \large s(course_id) = \Pi_{course_id}(\sigma_{\text{dept_name = 'Biology'}}(course)) $$
then $r \div s$ gives us students who have taken all courses offered by the Biology department.
Can write $r \div s$ as $$ temp1 \leftarrow \Pi_{R - S}(r) temp2 \leftarrow \Pi_{R - S}((temp1 \times s) - \Pi_{R - S, S}(r)) result = temp1 - temp2 $$
#Overview
#Extended relation algebra
#generalized projection
Extends the projection operation by allowing arithmetic functions to be used in the projection list
$$ \large \Pi_{F_1, F_2, \cdots, F_n}(E) $$
E is any relational-algebra expression Each of $F_1, F_2, \cdots, F_n$ are arithmetic expressions involving constants and attributes in the schema of E
Example: Given relation instructor(ID, name, dept_name, salary) where salary is annual salary, get the same information but with monthly salary $$ \large \Pi_{\text{ID, name, dept_name, salary/12}}(instructor) $$
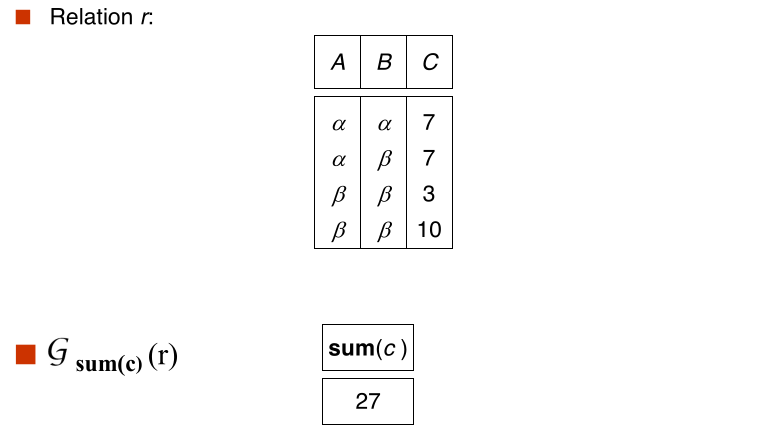
#aggregate functions and operations
-
Aggregate function takes a collection of values and returns a single values as result
- avg: average value
- min: minium value
- max: maximum value
- sum: sum of values
- count: number of values
-
Aggregate operation in relational algebra
$$ \large _{G_1, G_2, \cdots, G_n} \mathcal{G} _{F_1(A_1), F_2(A_2), \cdots, F_n(A_n)}(E) $$
E is any relational algebra operation
- $G_1, \cdots, G_n$ is a list of attributes on which to group(can my empty)
- Each $F_i$ is an aggregate function
- each $A_i$ is an attribute name
Note: some books/articles use $\gamma$ instead of $\mathcal{G}$
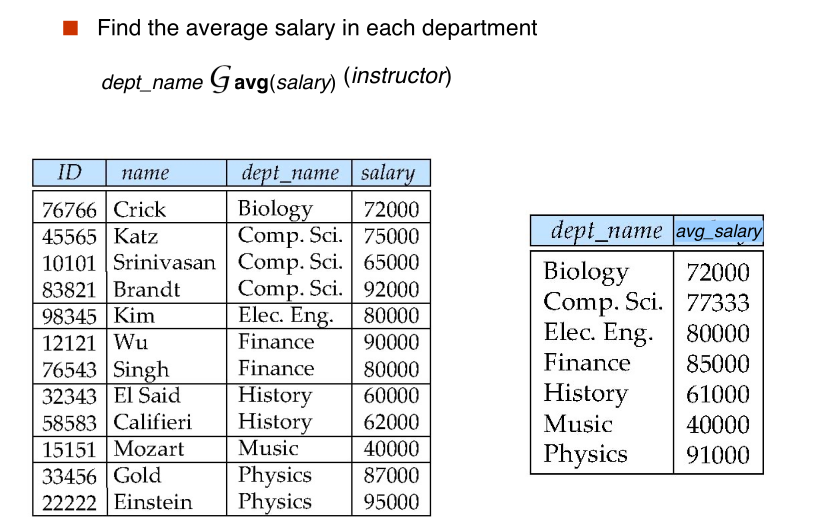
- Result of aggregation does not have a name
- Can use rename operation to give it a name
- For convenience, we permit renaming as part of aggregate operation

#Multiset Relational Algebra
Pure relational algebra removes all duplicates.
Multiset relational algebra retains duplicates, to match SQL semantics
- SQL duplicate retention was initially for efficiency, but is now a feature
Multiset relational algebra defined as follows
- selection: has as many duplicates of a tuple as in the input, if the tuple satisfies the selection
- projection: one tuple per input tuple, even if ie is a duplicate
- cross product: if there are m copies of t1 in r, and n copies of t2 in s, there are m x n copies of t1.t2 in r x s.
- other operators similarly defined
#RA examples
